
| Estimating blocking recall. Suppose we take one record from each set of duplicates as a query. Making a query into the records of a file results in the retrieval of those records that agree with the query in the fields chosen as blocking fields. Total blocking recall for a particular selection of key fields would be the average recall for all queries that might be made. |
| The only records that allow comparison with a query are ones with data in the corresponding field. The presence value (pi) of a field (i) may be calculated as the relative frequency of data occurring in the field. This is a good estimate of the probability of data occurring in the field. |
 | (3.1) |
| If we are going to compare every record with every other record, so as to identify duplicate (matching) records in a database, we cannot be sure that there will be data to query by. The probability that there would be data in both records would then be pi2. |
| Now in order to be in the same block as the query the data must also agree. We can get the probability that data agrees from the reliability. Each blocking field must, therefore, have data present and agreeing in order for the matched record to be brought back in the block. |
| The probability that the blocking scheme brings back matched records is thus the product of the probability that each of the fields (i) has data present (pi2) and that the values agree, i.e., the field is reliable (ri). This gives us equation 3.1 for blocking recall. |
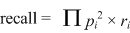 | (3.2) |
| The upper case Greek letter pi is the mathematical symbol for "product" and indicates that recall is a product of these values for all the blocking fields (i). We derive measures of reliability in the next few paragraphs. |
| An iterative method for estimating reliability. A good estimate of the reliability of a field is the relative frequency of agreement in comparisons between matched records. If it is not possible to get a measure of reliability from a set of matched records, it might be possible to estimate this value through performing record linkage iteratively as follows: |
| 1) Use an intuitive estimate of the reliability; |
| 2) perform record linkage with a high threshold, assuring that most linked records will be matched; |
| 3) measure the reliability of the weighting fields in the linked comparisons; |
| 4) repeat steps 1–3 until measure converges. |
| To get a reliability for blocking fields it would be crucial to iterate this whole iteration, using a different blocking scheme each time. This may result in smaller sets of comparisons and thus less confident measures of the reliability for these fields. |
| Measuring reliability. The measure of reliability is simple provided there is a set of matched pairs to measure against. |
 | (3.3) |
| The idea of a matched pair may be differently interpreted. First consider all cases of agreement in every possible comparison in all duplicate groups and assume further that every duplicate group is a matched pair. We might call this the comparison reliability, P(Ai |MC), i.e., the probability that the field data values agree in any matched comparison taken at random. |
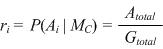 | (3.4) |
| We could also use equation 3.4 for duplicate groups consisting of more than two members. However, when the duplicate groups are large, the equation will give a bias to comparisons in those groups. The larger the group, the larger the number of comparisons possible, and the greater the probability that there will be agreement. It may be advisable, therefore, to take a weighted average of all duplicate groups with each linkage entity being equally important. This suggests a second measure of reliability that we could call the entity reliability, P(Ai |ME), i.e., the probability that the data in two corresponding fields belonging to all comparisons involving some randomly chosen linkage entity agree. |
| In this case we sum the relative frequency of agreement (Aij) among comparisons in the duplicate group representing each linkage entity (Cij), and divide it by the total number of groups (Gtotal). |
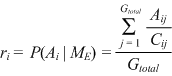 | (3.5) |
| The number of comparisons depends on the size of the duplicate group (Nj). It is the number of combinations taken two at a time. |
| Cij = [Nj × (Nj – 1)] ÷ 2 | (3.5) |
| Typically these two measures of reliability are very nearly the same. Only as there are greater numbers of larger duplicate groups would we expect them to diverge. |