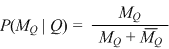
| A definition for blocking precision. Blocking precision is equal to matched records in query blocks (MQ) divided by the sum of the matched records in query blocks (MQ) and the unmatched records in query blocks (UQ). |
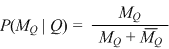 | (3.9) |
| With enough constraints it is pretty easy to determine how many queries there might be. To get a handle on precision we might select only duplicates to use for queries and not use the query unless there are data in the blocking fields. There would be just as many queries as represent duplicate groups (G) in proportion as the data would be present (pi) and in agreement (ri). |
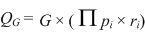 | (3.10) |
Matched records in blocks.
The matched records in query blocks (MQ) are the records that represent the same entity as the query.
This would have to be equal to the queries themselves plus the duplicates of the queries.
The duplicates in query blocks as indicated in equation 3.3 would be QG × P(DE) in proportion as the data is present and in agreement (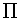 pi × ri ).
In other words we multiply the queries times one (for the query) plus the entity duplication rate (for its duplicates): pi × ri ).
In other words we multiply the queries times one (for the query) plus the entity duplication rate (for its duplicates): |
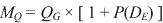 | (3.11) |
| The result of substituting for QG the value in equation 3.10 and for P(DE) the value in equation 3.4 expresses MQ in terms of the more basic values — equation 3.12. |
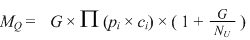 | (3.12) |
Unmatched records (noise) in blocks.
The unmatched records in query blocks (UQ) is the noise.
The noise is comprised of the non-duplicates.
This means that noise records are not duplicates of the query defining the block.
To be exact we must realize that noise may include duplicates of records in other blocks.
In other words the unmatched records in blocks are taken from the total records in the file.
All we need to do is subtract out one query and its duplicates ([1 + (G ÷ NG)] ~= 1 ) from the total number of records (Ntotal).
For large files this is essentially the total number of records (Ntotal – 1 ~= Ntotal).
Those unmatched records that actually fall in blocks do so in proportion as the data is present (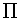 pi) and agrees ( pi) and agrees (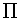 ci). ci). |
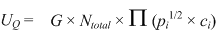 | (3.13) |
| We discuss the derivation of coincidence (c) in paragraph 3-6 below. |
A specific expression for blocking precision.
Now, when we substitute the values from equations 3.12 and 3.13 back into equation 3.9,
we note that the presence factor (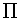 pi) and number of groups (queries) appear in every term.
Hence, we cancel them out.
Then we note also that the reliability factor appears in two of the three terms.
This allows a “simplification” resulting in the equation in 3.14. pi) and number of groups (queries) appear in every term.
Hence, we cancel them out.
Then we note also that the reliability factor appears in two of the three terms.
This allows a “simplification” resulting in the equation in 3.14. |
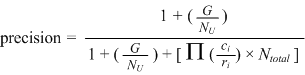 | (3.14) |
| This precision is for a blocking scheme. If we wonder about the block size for specific values in the blocking fields we would use the version of the coincidence that is specific to that value. |
| An iterative approach to blocking precision. As discussed for reliability in 3-1.2 precision may possibly also be determined without a predefined set of matched records. The coincidence is the measured estimate, and the reliability, the intuitive estimate. The number of groups related to the unique records may begin at a small enough estimate that the precision estimate will converge with each pass. After the first pass these may be measured for each subsequent pass. |
| Measuring coincidence. The field’s coincidence (coincidental agreement) is defined as the probability that the field values agree in non-matched pairs, i.e., by chance, which coincidence is different for each specific value. |
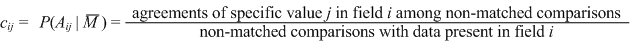
| As it turns out in practice, it is not straight-forward to take direct measures of the quantities indicated in the above equation. So, first we estimate the probability of each field value occurring in a record by measuring its relative frequency in the database (B-value), which, when the duplication rate is not too high, is very close to its relative frequency in one record of a non-matched pair. |
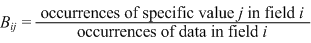
| The square the B-value for each field value would then be an estimate of its value-specific coincidental agreement in a comparison. |

| We then sum of the squares of the B-value of each possible field value to estimate the field’s coincidental agreement in a comparison. |
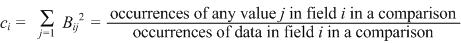
| Note that the revision to reliability that we made in ¶ 3-1.3, equation 3.3, does not improve the theoretical precision. However, in the same way as the measure of duplication rate and reliability are ambiguous, so is also coincidence. As we see above, coincidence may be the proportion of comparisons either as tallied 1) across non-matched comparisons, or 2) across all comparisons possible (with data present). In the latter case we might make the following refinement: take a fractional agreement when the comparison includes records out of a duplicate group, i.e., where there are several possible within the same linkage entity. We might then call the coincidence involving an unrefined tally a general coincidence, i.e., the probability that a field value agrees in a comparison taken at random provided only that data is present in the field. The refinement would then be the entity coincidence, i.e., the probability that a field value agrees in a comparison taken at random provided 1) that data is present in the field, and 2) each comparison is counted only in proportion as it represents a uniquely significant record linkage entity. |
| Accidental agreement depends on the specific value in the field. The value is more likely to agree when it is common than when it is rare. In fact, the probability of the field agreeing in a comparison is simply the sum of all the probabilities of each specific value agreeing. But the calculation of this B-value and its general coincidence does not regard whether the record is a singleton or belongs to a group. In the case of entity coincidence we first tally the presence (P = occurrences = tokens) of each specific value (the index j = type) within a duplicate group (entity), weighting it as a single entity, then tally the entity frequencies. The index on the innermost sigma is k running from 1 to Cijl (combinations), which equals = 1 for singletons. The index on the second sigma is l running through the duplicate groups including singletons to NU (uniquely significant records). In this way each entity counts its value but once. These are then squared as comparisons and then summed to result in total agreements in comparisons. |
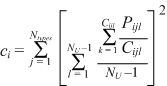 | (3.15) |
| Using the total number of uniquely significant records actually omits the fact that we want to exclude all comparisons of a record to itself. For precision we subtract one (1) from this number. Typically, and especially when there are large numbers of duplicates, the entity coincidence is smaller than the general coincidence. Specific data values are shown to be more distinctive than they otherwise would be estimated to be. |