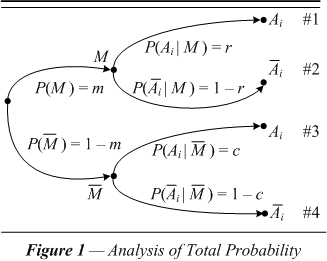
| Odds of field value agreement. Refer now to figure 4 of the first chapter as here augmented in figure 1. |

| These figures illustrate Bayes’ theorem as it relates to record linkage. The probability of field value agreement when the comparison is matched is here related to the probability that it agrees in any event. This is the agreement ratio. It follows from the theorem of total probability that the probability of the data agreeing is #1 + #3. Branch #1 is the probability of agreement when matched as represented by the reliability; branch # 3 is a probability of agreement when unmatched as represented by the coincidence. The agreement ratio is #1 ÷ (#1 + #3). |
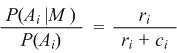
| The agreement odds, which we give in equation (4.2), translates directly from the agreement ratio. |
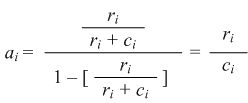 | (4.2) |
| Odds of field value disagreement. From the theorem of total probability it follows that disagreement ratio be #2 ÷ (#2 + #4). Similarly the disagreement odds translate directly from the disagreement ratio: |
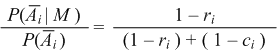
| This then gives us the disagreement odds in equation (4.3). As the value of the probability that the comparison is a match approaches zero, these odds also diminish, though the coincidence value becomes more important. |
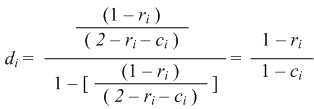 | (4.3) |
| Odds of field value missing. If there is data or no data in one or both of the fields being compared, this fact alone tells us nothing. We assume that the distribution of blanks and data are the same, whether the comparison is among the matched or the whole file. The presence and absence frequency ratios are both one (1). |
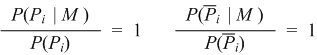
| Hence we have the odds that the comparison of a field appears blank in equation (4.4): |
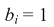 | (4.4) |
| Changing odds to weights. To simplify the mathematics further it is possible to take the logarithm of the adjusted odds so as to get field weights. We multiply probabilities together to yield a total probability. The product of the odds is directly proportional to the total probability. |
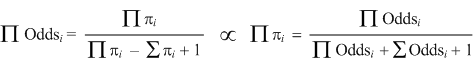 | (4.5a) |
| We add their logarithms together to yield a sum that then represents the logarithm of the product of the odds, viz., the probabilities. |
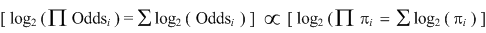 | (4.5b) |
| When we choose to use two as the base of the logarithms, we have a binit weight. The field’s weight for agreement (awi) is therefore, |
| awi = log2 (ai) | (4.6) |
| The field’s weight for disagreement (dwi ) is similarly, |
| dwi = log2 (di) | (4.7) |
| And, of course, when the value is missing the weight contributes nothing: |
| bwi = log2 (bi) = 0 | (4.8) |
| If the field values are independent, the principle of independent probilities (cf. 2-2.5) allows us to conclude: the sum of the weights of the odds for each field will be proportional to the probability of them occurring in that combination of agreement, disagreement, and being missing. In this way we add field weights to yield a record comparison weight. Because we use the principle of independent probabilities, it is very important to consider the independence of the data between the fields to be weighted. We discuss this concern in chapter 5. |
| Calculating record comparison weights. To calculate the comparison weight for the whole record, we may now add together the weights for all the fields chosen (cwi). If the field agrees, that field’s contribution to the record comparison weight will be the agreement weight from equation (4.6). In the case where the field disagrees (though data is present in both fields), that field’s contribution to the record comparison weight will be the disagreement weight from equation (4.7). The field’s contribution when there is data missing in one or both records is from equation (4.8). |
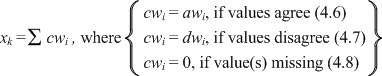 | (4.9) |
| The record comparison weight (xk) has a different value for each combination (k) of fields being in agreement, disagreement, or missing. One combination, say k = 1, is all fields being present and agreeing. There are three different values that cwi might have. If n is the number of fields weighted, then the number of combinations (m) would be 3n. So the final cwi, say cwk, where k = m, is all fields missing, i.e., 0. |