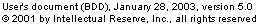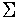 awi =Xk | M ) = apk
awi =Xk | M ) = apk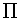 arki
arki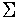 dwi =Xk | M ) = apk
dwi =Xk | M ) = apk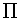 ( 1 - arki )
( 1 - arki )| There are two probabilities of a particular comparison weight occurring. The first is when the comparison is between matched records and the second is when it is between unmatched records. In order to make these probabilities independent of whether the comparison weight is matched or unmatched we need to multiply by the probability that it falls into one or the other of these categories. |
| Probability of a matched comparison weight occurring. We may state the probability of occurrence for a particular comparison weight as directly proportional to the adjusted presence (apk) for the combination (k) of individual field weights. The probability of the comparison weight occurring in matched records when all fields agree is related to the adjusted reliability as in equation 6.1. When they disagree this probability relates to the complement of the adjusted reliability as in equation 6.2. When the data are all missing it is independent of either the reliability or the coincidence, but equal to the adjusted presence as in equation 6.3. |
P(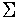 awi =Xk | M ) = apk awi =Xk | M ) = apk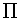 arki arki | (6.1) | ||
P(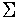 dwi =Xk | M ) = apk dwi =Xk | M ) = apk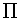 ( 1 - arki ) ( 1 - arki ) | (6.2) | ||
| P( 0 =Xk | M ) = apk | (6.3) |
It is possible to combine this set of equations into a single simpler one if we symbolize those parts that are different with the same letter, say R.
We then make the stipulation that R consists of three factors:
R1 = 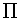 arki, being the k1 fields that agree;
R2 = arki, being the k1 fields that agree;
R2 = 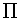 (1 – arki) being the k2 fields that disagree;
and R3 = 1 for the k3 fields where at least one value is missing.
This allows one to combine equations 6.1 and 6.2 with 6.3 as equation 6.4 — the probability of occurrence (yRk) for a particular matched comparison weight ( (1 – arki) being the k2 fields that disagree;
and R3 = 1 for the k3 fields where at least one value is missing.
This allows one to combine equations 6.1 and 6.2 with 6.3 as equation 6.4 — the probability of occurrence (yRk) for a particular matched comparison weight (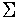 cw): cw): |
yRk = P(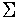 cwi =Xk | M ) = apk × cwi =Xk | M ) = apk × 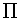 Rj Rj | (6.4) |
| With these equations in mind we can write an algorithm to calculate the probability that a particular comparison weight will occur in a matched comparison. |
| Probability of an unmatched comparison weight occurring. In a completely analogous fashion it is possible to estimate the corresponding probability for unmatched comparison weights. In this case each agreement weight occurs in proportion to the coincidence value (acki) and each disagreement weight occurs in proportion as one minus the coincidence value. Here we symbolize the three cases with C and express the probability of a particular comparison weight (zCk) as in equation 6.5: |
yCk = P(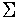 cwi =Xk | U ) = apk × cwi =Xk | U ) = apk × 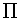 Cj Cj | (6.5) |
| Probability of a comparison weight being matched. In order to make these probabilities independent of whether the comparison weight is matched or unmatched it is important to multiply by the probability that it falls into one or the other of these categories. The first is the probability that a comparison weight is matched, P(M). The numerator of this value, the number of matched comparison weights (WM), would be equal to the number of matched records in blocks of equation 2.9 (MQ), and the denominator the sum of matched and unmatched records. |
| P(M) = WM ÷ (WM + WU) where WM = MQ | (6.6) |
| Probability of a comparison weight being unmatched. The second is the probability that a comparison weight is unmatched, P(U). The numerator of this value is the number of unmatched comparison weights (WU). We can derive this value from equation 6.6 as soon as we realize that P(M), the probability of a weight being matched, is, in our situation, exactly equal to the blocking precision, which we estimated with equation 3.12 (see also equation 6.10 below). |
| WU = [ WM ÷ P(M) ] – WM where WM = MQ | (6.7) |
| The second probability would therefore be: |
| P(U) = WU ÷ (WM + WU) | (6.8) |