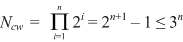Preliminary adjustment calculations.
A chain of three fully dependent fields results in eight combinations:
 1 = [ ], i.e., no fields (dis)agree, 1 = [ ], i.e., no fields (dis)agree,  2 = [ 1 ], i.e., only the most dependent field (dis)agrees, 2 = [ 1 ], i.e., only the most dependent field (dis)agrees,
 3 = [ 2 ], i.e., only less dependent field (dis)agrees, 3 = [ 2 ], i.e., only less dependent field (dis)agrees,  4 = [ 3 ], i.e., only independent field (dis)agrees, 4 = [ 3 ], i.e., only independent field (dis)agrees,
 5 = [ 1, 2 ], i.e., dependent fields (dis)agree, 5 = [ 1, 2 ], i.e., dependent fields (dis)agree,  6 = [ 1, 3 ], i.e., only most dependent and independent fields (dis)agree, 6 = [ 1, 3 ], i.e., only most dependent and independent fields (dis)agree,
 7 = [ 2, 3 ], i.e., less dependent and independent fields (dis)agree, 7 = [ 2, 3 ], i.e., less dependent and independent fields (dis)agree,  8 = [ 1, 2, 3 ], i.e., all three fields (dis)agree.
As pointed out in 4-19, the adjusted reliability and coincidence on only four of these is non-zero: 8 = [ 1, 2, 3 ], i.e., all three fields (dis)agree.
As pointed out in 4-19, the adjusted reliability and coincidence on only four of these is non-zero:
 1 = [ ], i.e., no fields (dis)agree, 1 = [ ], i.e., no fields (dis)agree,
 4 = [ 3 ], i.e., only independent field (dis)agrees, 4 = [ 3 ], i.e., only independent field (dis)agrees,
 7 = [ 2, 3 ], i.e., less dependent and independent fields (dis)agree, and 7 = [ 2, 3 ], i.e., less dependent and independent fields (dis)agree, and
 8 = [ 1, 2, 3 ], i.e., all three fields (dis)agree.
We also pointed out that when we compare two records their various comparisons are then grouped into four (dis)agreement cases;
these cases we then refer to as ar0, ar1, ar2, ar3 and ac0, ac1, ac2, ac3.
These values are arranged on table 2 as some of the raw data needed before we can begin probability calculations involving value dependent fields. 8 = [ 1, 2, 3 ], i.e., all three fields (dis)agree.
We also pointed out that when we compare two records their various comparisons are then grouped into four (dis)agreement cases;
these cases we then refer to as ar0, ar1, ar2, ar3 and ac0, ac1, ac2, ac3.
These values are arranged on table 2 as some of the raw data needed before we can begin probability calculations involving value dependent fields. |
 1 = [ ], i.e., no fields (dis)agree,
1 = [ ], i.e., no fields (dis)agree,  2 = [ 1 ], i.e., only the most dependent field (dis)agrees,
2 = [ 1 ], i.e., only the most dependent field (dis)agrees,
 3 = [ 2 ], i.e., only less dependent field (dis)agrees,
3 = [ 2 ], i.e., only less dependent field (dis)agrees,  4 = [ 3 ], i.e., only independent field (dis)agrees,
4 = [ 3 ], i.e., only independent field (dis)agrees,
 5 = [ 1, 2 ], i.e., dependent fields (dis)agree,
5 = [ 1, 2 ], i.e., dependent fields (dis)agree,  6 = [ 1, 3 ], i.e., only most dependent and independent fields (dis)agree,
6 = [ 1, 3 ], i.e., only most dependent and independent fields (dis)agree,
 7 = [ 2, 3 ], i.e., less dependent and independent fields (dis)agree,
7 = [ 2, 3 ], i.e., less dependent and independent fields (dis)agree,  8 = [ 1, 2, 3 ], i.e., all three fields (dis)agree.
As pointed out in 4-19, the adjusted reliability and coincidence on only four of these is non-zero:
8 = [ 1, 2, 3 ], i.e., all three fields (dis)agree.
As pointed out in 4-19, the adjusted reliability and coincidence on only four of these is non-zero:
 1 = [ ], i.e., no fields (dis)agree,
1 = [ ], i.e., no fields (dis)agree,
 4 = [ 3 ], i.e., only independent field (dis)agrees,
4 = [ 3 ], i.e., only independent field (dis)agrees,
 7 = [ 2, 3 ], i.e., less dependent and independent fields (dis)agree, and
7 = [ 2, 3 ], i.e., less dependent and independent fields (dis)agree, and
 8 = [ 1, 2, 3 ], i.e., all three fields (dis)agree.
We also pointed out that when we compare two records their various comparisons are then grouped into four (dis)agreement cases;
these cases we then refer to as ar0, ar1, ar2, ar3 and ac0, ac1, ac2, ac3.
These values are arranged on table 2 as some of the raw data needed before we can begin probability calculations involving value dependent fields.
8 = [ 1, 2, 3 ], i.e., all three fields (dis)agree.
We also pointed out that when we compare two records their various comparisons are then grouped into four (dis)agreement cases;
these cases we then refer to as ar0, ar1, ar2, ar3 and ac0, ac1, ac2, ac3.
These values are arranged on table 2 as some of the raw data needed before we can begin probability calculations involving value dependent fields. 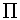 apki × arki
apki × arki